Charakterisierung mehrdimensionaler Verteilungen  Wahrscheinlichkeitstheorie  Charakterisierung von Verteilungen

Zufallsvektoren

Zufallsvektor
Komponenten des Zufallsvektors
gemeinsames Wahrscheinlichkeitsmaß
gemeinsame (kumulative) Verteilungsfunktion
Randverteilungsfunktion
N-dimensionaler diskreter Zufallsvektor
gemeinsame diskrete Verteilungsfunktion
gemeinsame diskrete Dichtefunktion
diskrete Randdichtefunktion
N-dimensionaler stetiger Zufallsvektor
gemeinsame Dichtefunktion
gemeinsame absolut stetige Verteilungsfunktion
stetige Randdichtefunktion
bedingte diskrete Dichtefunktion
bedingte diskrete (kumulative) Verteilungsfunktion
bedingte stetige Dichtefunktion
bedingte stetige (kumulative) Verteilungsfunktion
(stochastisch) unabhängig

Ein Zufallsvektor  auf dem Wahrscheinlichkeitsraum  ist eine Zusammenfassung von N Zufallsvariablen  auf den Wahrscheinlichkeitsräumen  ,  . Die einzelnen Zufallsgrößen  nennt man Komponenten des Zufallsvektors X. Die Komponenten  müssen dabei auf ein und demselben Meßraum definiert sein, die Wahrscheinlichkeitsmaße können unterschiedlich sein. Das Wahrscheinlichkeitsmaß P heißt gemeinsames Wahrscheinlichkeitsmaß der Zufallsvariablen  ,  . Aus dem Wahrscheinlichkeitsmaß P lassen sich alle Wahrscheinlichkeitsmaße  ,  , berechnen. Die Umkehrung gilt im allgemeinen nicht (Ausnahme: stochastische Unabhängigkeit der Komponenten!).

Die gemeinsame (kumulative) Verteilungsfunktion  eines Zufallsvektors  von Zufallsvariablen  ,  ist definiert als:

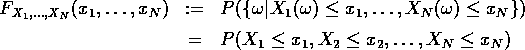
für alle reellen  , n=1,...,N.

Wenn  die gemeinsame Verteilungsfunktion von X und Y ist, dann werden die Verteilungsfunktionen

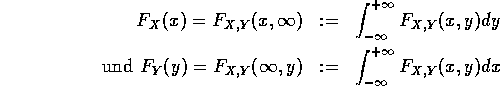
Randverteilungsfunktionen von X bzw. Y genannt. Diese sind die individuellen Verteilungsfunktionen von X bzw. Y.

Ein N-dimensionaler Zufallsvektor  heißt N-dimensionaler diskreter Zufallsvektor, wenn er mit positiver Wahrscheinlichkeit höchstens abzählbar viele Wertetupel  annimmt.
Wenn ein Zufallsvektor diskret ist, dann heißt auch die dazugehörige gemeinsame Verteilungsfunktion diskret.
Die Funktion

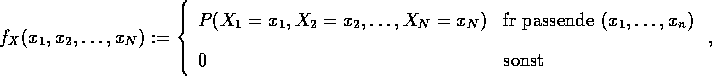
wobei  die h”chstens abzählbar vielen Wertetupel des diskreten Zufallsvektors X mit positiver Wahrscheinlichkeit sind, heißt gemeinsame diskrete Dichtefunktion des N-dimensionalen diskreten Zufallsvektors X.

Wenn  die gemeinsame diskrete Dichtefunktion von (X,Y) mit Wertetupeln  ,  , ist, dann werden die diskreten Dichtefunktionen

diskrete Randdichtefunktionen von X bzw. Y genannt.

Ein Zufallsvektor  heißt N-dimensionaler stetiger Zufallsvektor, wenn eine Funktion  existiert, so daß gilt:

Die Funktion  heißt gemeinsame Dichtefunktion der Zufallsvariablen  . Die zu einem stetigen Zufallsvektor gehörende gemeinsame Verteilungsfunktion heißt absolut stetig.

Wenn (X,Y) ein 2-dimensionaler stetiger Zufallsvektor ist, dann werden die Dichtefunktionen

stetige Randdichtefunktionen von X bzw. Y genannt.

Äquivalent zu den bedingten Wahrscheinlichkeiten ist auch die Veränderung der Verteilung einer Zufallsvariablen Y interessant, falls das Ereignis (X=x) bereits eingetreten ist. Dies führt zur Definition der bedingten Dichtefunktion und der bedingten Verteilungsfunktion.
Seien X,Y diskrete Zufallsvariablen mit der gemeinsamen diskreten Dichtefunktion  . Die bedingte diskrete Dichtefunktion von Y gegeben (X=x) ist definiert durch:

für  , wobei  Randdichte von X an der Stelle x ist.
Die bedingte diskrete (kumulative) Verteilungsfunktion von Y gegeben (X=x) ist definiert durch:

für  , wobei  Randdichte von X an der Stelle x ist.
Seien X,Y stetige Zufallsvariablen mit der gemeinsamen stetigen Dichtefunktion  . Die bedingte stetige Dichtefunktion von Y gegeben (X=x) ist definiert durch:

für  , wobei  Randdichte von X an der Stelle x ist.
Die bedingte stetige (kumulative) Verteilungsfunktion von Y gegeben (X=x) ist definiert durch:

für  , wobei  Randdichte von X an der Stelle x ist.

Die Zufallsvariablen  heißen (stochastisch) unabhängig,

(i)

wenn für die gemeinsame Verteilungsfunktion  der Zufallsvariablen  gilt:

für alle  ,

(ii)

bzw. wenn für diskrete oder stetige Zufallsvariablen  mit der gemeinsamen Dichte  gilt:

für alle  .

• Charakterisierung mehrdimensionaler Verteilungen

  
 Charakterisierung mehrdimensionaler Verteilungen  Wahrscheinlichkeitstheorie  Charakterisierung von Verteilungen
 
Fri Feb 20 16:16:46 MET 1998