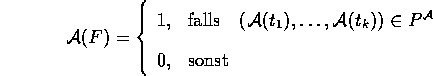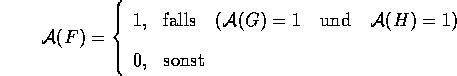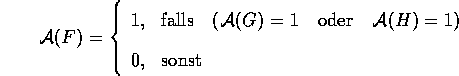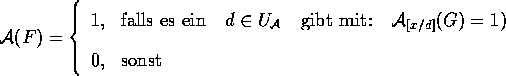

Up: Logik
Previous: Aussagenlogik
Prädikatenlogik
|
Chronologisch
|
Alphabetisch
|
|
|
|
Die Prädikatenlogik ist eine Erweiterung der Aussagenlogik, wobei
Quantoren, Funktions- und Prädikatsymbole hinzukommen. Durch diese
Konzepte sind Sachverhalte beschreibbar, die im Rahmen der Aussagenlogik
nicht formuliert werden können. In der Aussagenlogik war es z.B. nicht
möglich auszudrücken, daß gewisse ``Objekte`` in Beziehung
stehen; daß eine Eigenschaft für alle Objekte gilt, oder daß
ein Objekt mit einer gewissen Eigenschaft existiert.
Syntax
der Prädikatenlogik
Eine (prädikatenlogische) Signatur S ist ein Tupel 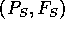 , wobei
, wobei 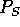 und
und 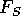 endliche oder abzählbar unendliche Mengen sind mit
endliche oder abzählbar unendliche Mengen sind mit 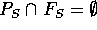 und
und 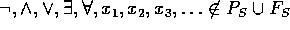 .
.
Eine Variable hat die Form 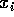 mit
mit 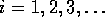 . Ein Prädikatsymbol
hat die Form
. Ein Prädikatsymbol
hat die Form 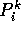 und ein Funktionssymbol hat die
Form
und ein Funktionssymbol hat die
Form 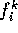 mit
mit 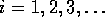 und
und 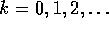 . Hierbei
heißt i jeweils der Unterscheidungsindex und k die Stellenzahl
oder Stelligkeit. Man definiert
die Menge der Terme
. Hierbei
heißt i jeweils der Unterscheidungsindex und k die Stellenzahl
oder Stelligkeit. Man definiert
die Menge der Terme 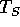 durch einen induktiven Prozeß:
durch einen induktiven Prozeß:
-
Jede Variable ist ein Term.
-
Falls f ein Funktionssymbol ist mit Stellenzahl k und falls
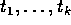 Terme sind, so ist auch
Terme sind, so ist auch 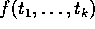 ein Term.
ein Term.
Hierbei sollen auch Funktionssymbole der Stellenzahl 0 eingeschlossen sein,
und in diesem Fall sollen die Klammern wegfallen. Nullstellige Funktionssymbole
heißen auch Konstanten.
Nun kann man die Menge der prädikatenlogischen
Formeln 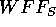 definieren:
definieren:
-
Falls P ein Prädikatsymbol der Stelligkeit k ist, und falls
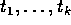 Terme sind, dann ist
Terme sind, dann ist 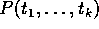 eine Formel.
eine Formel.
-
Für jede Formel F ist auch
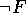 eine Formel.
eine Formel.
-
Für alle Formeln F und G sind auch
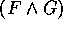 und
und 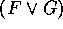 Formeln.
Formeln.
-
Falls x eine Variable ist und F eine Formel, so sind auch
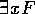 und
und 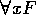 Formeln.
Formeln.
Atomare Formeln nennt man genau die
Formeln, die gemäß i) aufgebaut sind. Falls F eine Formel ist
und F als Teil einer Formel G auftritt, so heißt F Teilformel von
G.
Sematik der
Prädikatenlogik
Eine Struktur ist ein Paar 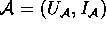 ,
wobei
,
wobei 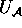 eine
beliebige aber nicht leere Menge ist, die Grundmenge
oder Universum von
eine
beliebige aber nicht leere Menge ist, die Grundmenge
oder Universum von 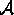 genannt wird. Ferner ist
genannt wird. Ferner ist 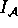 eine Abbildung, die
eine Abbildung, die
-
jedem k-stelligen Prädikatsymbol P (das im Definitionsbereich von
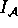 liegt) ein k-stellliges Prädikat über
liegt) ein k-stellliges Prädikat über 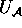 zuordnet,
zuordnet,
-
jedem k-stelligen Funktionssymbol f (das im Definitionsbereich von
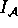 liegt) eine k-stellige Funktion auf
liegt) eine k-stellige Funktion auf 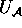 zuordnet,
zuordnet,
-
jeder Variablen x (sofern
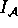 auf x definiert ist) ein Element der Grundmenge
auf x definiert ist) ein Element der Grundmenge 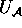 zuordnet.
zuordnet.
Sei F eine Formel und 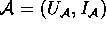 eine Struktur.
eine Struktur. 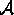 heiát zu F passend, falls
heiát zu F passend, falls 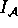 für alle in F vorkommenden Prädikatsymbole, Funktionssymbole
und freien Variablen definiert ist.
für alle in F vorkommenden Prädikatsymbole, Funktionssymbole
und freien Variablen definiert ist.
Sei F eine Formel und 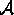 eine zu F passende Struktur. Für jeden Term t, den man aus den Bestandteilen
von F bilden kann, definiert man den Wert von
t in der Struktur
eine zu F passende Struktur. Für jeden Term t, den man aus den Bestandteilen
von F bilden kann, definiert man den Wert von
t in der Struktur 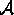 , den man mit
, den man mit 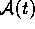 bezeichnet.
Der Fall ii) schließt auch die Möglichkeit ein, daß f
nullstellig ist, also t die Form hat t=a. In diesem Fall ist also
bezeichnet.
Der Fall ii) schließt auch die Möglichkeit ein, daß f
nullstellig ist, also t die Form hat t=a. In diesem Fall ist also 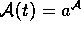 . Auf analoge Weise definiert man den Wahrheitswert
der Formeln F unter der Struktur
. Auf analoge Weise definiert man den Wahrheitswert
der Formeln F unter der Struktur 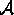 , wobei man ebenfalls die Bezeichnung
, wobei man ebenfalls die Bezeichnung 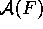 verwendet.
Hierbei ist
verwendet.
Hierbei ist 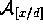 diejenige Struktur
diejenige Struktur 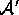 , die überall mit
, die überall mit 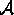 identisch ist, bis auf die Definition von
identisch ist, bis auf die Definition von 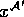 : Es sei nämlich
: Es sei nämlich 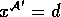 , wobei
, wobei 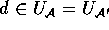 -
unabhängig davon, ob
-
unabhängig davon, ob 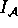 auf x definiert ist oder nicht.
auf x definiert ist oder nicht.
Die Prädikatenlogik ist in folgendem Sinn eine Erweiterung der
Aussagenlogik: Falls alle Prädikatsymbole nullstellig sein müssen
erhält man Formeln der Aussagenlogik, wobei die nullstelligen Prädikatsymbole
die Rolle der atomaren Formeln der Aussagenlogik übernehmen.
Die Begriffe ``Folgerbarkeit``, ``Modell``
und ``erfüllbar`` lassen sich direkt
aus der Aussagenlogik übertragen.
Für die Ableitbarkeit kommen
weitere logische Axiome zu denen der Aussagenlogik hinzu. Ausserdem gibt
es eine weitere Ableitungsregel, nämlich das Generalisieren.
Substitution
Sei S eine Signatur, s ein Term aus 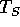 und x eine Variable.
und x eine Variable.
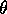 -Subsumtion
-Subsumtion
Als Grundlage für die Generalisierungsrelation
kann der Forgerungsbegriff verwendet werden. Da die Folgerbarkeit im
allgemeinen Fall aber nicht entscheidbar ist, wird die schwächere
Subsumtionsbeziehung bevorzugt. Immer, wenn die Subsumtionsbeziehung gilt,
gilt auch die logische Folgerung - aber nicht umgekehrt!
Eine Klausel C1 ist genereller als eine andere Klausel C2,
wenn gilt: C1 subsumiert C2.
Für Literale gilt:
Ein Literal L1 subsumiert ein anderes Literal L2, wenn es eine
Substitution 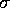 gibt, so daß
gibt, so daß 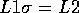 .
.
Damit wird die Substitution zur Grundlage der Formalisierung der Generalisierung.
Für Hornklauseln gilt folgende Definition der 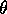 -Subsumtion:
-Subsumtion:
Eine Hornklausel 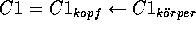
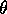 -subsumiert eine Hornklausel
-subsumiert eine Hornklausel 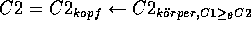 , gdw. es eine Substitution
, gdw. es eine Substitution 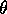 gibt, so daß
gibt, so daß 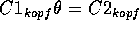 , und
, und 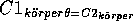 .
.
Generalisierte 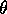 -Subsumtion
-Subsumtion
Die generalisierte 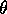 -Subsumtion generalisiert zwei funktionsfreie Hornklauseln bezüglich
gegebenem Hintergrundwissen. Die Substitution
-Subsumtion generalisiert zwei funktionsfreie Hornklauseln bezüglich
gegebenem Hintergrundwissen. Die Substitution 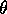 führt für alle Variablen der zu generalisierenden Klausel neue
Konstante ein.
führt für alle Variablen der zu generalisierenden Klausel neue
Konstante ein. 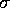 bezeichne eine Substitution von Termen. Dann ist die Generalisierung nach
Buntine folgendermaßen definiert:
bezeichne eine Substitution von Termen. Dann ist die Generalisierung nach
Buntine folgendermaßen definiert:
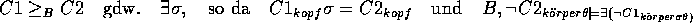
Operationalisierung der Definition:
Jede Klausel 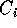 der generelleren Klauselmenge kann zurückgeführt werden auf eine
Klausel der spezielleren Klauselmenge, indem
der generelleren Klauselmenge kann zurückgeführt werden auf eine
Klausel der spezielleren Klauselmenge, indem
-
Variablen aus
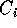 in Konstante oder andere Terme überführt werden,
in Konstante oder andere Terme überführt werden,
-
Atome dem Klauselkörper von
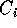 hinzugefügt werden, oder
hinzugefügt werden, oder
-
der Klauselkörper von
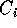 im Hinblick auf das Hintergrundwissen B teilweise ausgewertet wird, d.h.
ein Atom aus
im Hinblick auf das Hintergrundwissen B teilweise ausgewertet wird, d.h.
ein Atom aus 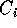 wird mit einer Klausel aus B resolviert.
wird mit einer Klausel aus B resolviert.
Die generalisierte Subsumtion ist nur für eingeschränkte Sprachklassen
entscheidbar.
Beschränkungen
von Hornklauseln
-
Eine Klausel ist generativ, wenn jede
Variable aus dem Klauselkopf auch im Klauselkörper vorkommt (
 bereichsbeschränkte Klauseln in deduktiven Datenbanken).
bereichsbeschränkte Klauseln in deduktiven Datenbanken).
-
Eine Klausel ist bezüglich B deterministisch,
wenn für jedes Literal im Klauselkörper die bereits durch Konstante
substituierten Variablen und das Hintergrundwissen eine eindeutige Substitution
für die restlichen Variablen des Literals festlegen. Gibt es mehr
als eine Sustitution, so ist die Klausel indeterministisch.
-
Eine Klausel ist beschränkt
(constrained), wenn jede Variable
aus dem Klauselkörper auch im Klauselkopf vorkommt.
k-lokale Hornklauseln
Sei D eine Hornklausel, 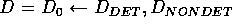 und vars eine Funktion, die die Menge der Variablen einer Klausel berechnet.
und vars eine Funktion, die die Menge der Variablen einer Klausel berechnet. 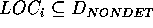 ist ein lokaler Teil von D genau dann, wenn
ist ein lokaler Teil von D genau dann, wenn 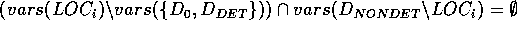 und es kein
und es kein 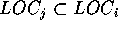 gibt, welches auch ein lokaler Teil von D ist. Ein lokaler Teil
gibt, welches auch ein lokaler Teil von D ist. Ein lokaler Teil 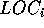 ist für eine Konstante k:
ist für eine Konstante k:
k-vlokaler Teil gdw. 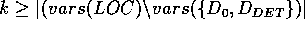 ,
,
k-llokaler Teil gdw. 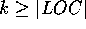 .
.
Eine Hornklausel D heißt k-llokal
genau dann, wenn jeder lokale Teil von D ein k-llokaler bzw. ein k-vlokaler
Teil ist.
Eine Klausel ist k-lokal, wenn sie
einen lokalen Teil von Variablen oder Literalen hat, der k-llokal oder
k-vlokal ist.
Deterministische
Tiefe eines Terms
Ein Term aus einem Klauselkopf K ist mit einer Kette der Länge
0 verbunden. Für den Klauselkörper nimmt man an, daß die
Literale nach ihrer Verbundenheit mit dem Klauselkopf geordnet sind: 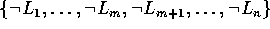 . Ein Term t aus
. Ein Term t aus 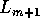 ist genau dann durch eine deterministische Kette der Länge d+1 verbunden,
wenn
ist genau dann durch eine deterministische Kette der Länge d+1 verbunden,
wenn
-
alle Terme im Klauselkopf und in
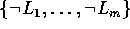 verbunden sind durch deterministische Ketten, die höchstens d lang
sind, und
verbunden sind durch deterministische Ketten, die höchstens d lang
sind, und
-
es für jede Substitution
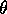 , die K mit einem Beispiel und die ersten Literale mit dem Hintergrundwissen
unifiziert - also
, die K mit einem Beispiel und die ersten Literale mit dem Hintergrundwissen
unifiziert - also 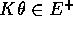 und
und 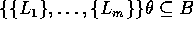 - genau
eine eindeutige Substitution
- genau
eine eindeutige Substitution 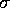 gibt, so daá
gibt, so daá 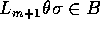 .
.
Die minimale Länge der deterministisch verbindenden Ketten ist die
determinsistische Tiefe eines Terms.
Eine Klausel ist ij-deterministisch,
wenn sie
Logik-Programmierung
Das Ausführen eines Programms kann aufgefaßt werden als das
(automatische) Herleiten der leeren Klausel aus einer gegebenen Klauselmenge,
zusammen mit einer Antworterzeugungskomponente. Die aus dem Resolutionsbeweis
extrahierte Antwort kann dann als Rechenergebnis des (Logik-) Programms
aufgefaát werden.
Sei eine i.a. erfüllbare Klauselmenge F gegeben. Dieses F kann
man als ein (Logik-) Programm auffassen: In F kommen gewisse Prädikate
und Funktionen vor und es werden durch die Klauseln in F gewisse Aussagen
über deren Beziehung zueinander gemacht.
Es soll durch die Logik-Programmierung nicht nur die Frage, ob die Existenz
eines (oder mehrerer) Objekte mit gewissen Eigenschaften aus dem Programm
F folgt, vom Auswertungsmechanismus mit ja oder nein beantwortet werden.
Es soll vielmehr im ja-Fall ein entsprechendes Objekt (oder möglicherweise
alle) ausgegeben werden.
Man will z.B. wissen, ob G aus F folgt. Dazu testet man mittels Resolution,
ob 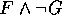 unerfüllbar
ist.
unerfüllbar
ist.

Up: Logik
Previous: Aussagenlogik
Uschi Robers
6.2.1998
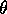 -Subsumtion
-Subsumtion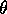 -Subsumtion
-Subsumtion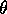 -Subsumtion
-Subsumtion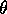 -Subsumtion
-Subsumtion